MANUSCRITO ENVIADO À BIBLIOTECA NACIONAL EM 1993 PARA SOLICITAÇÃO DE REGISTRO DE DIREITO AUTORAL
DOWNLOADOndas de De Broglie e as Órbitas Planetárias: Perspectivas Para Uma Cosmologia Quântica
Marçal de Oliveira Neto
Departamento de Química
Universidade de Brasília
Apresentação
O autor propõe-se discutir os conceitos que regem os nossos Universos ditos “Infinitamente Grande” e “Infinitamente Pequeno” e refletir a questão da observação sobre esse Universos. Tal observação leva-o a concluir que não existindo um olhar absoluto sobre a Natureza, o que é chamado de “Infinitamente Grande” pode se transformar em “Infinitamente Pequeno” quando se observa o nosso Cosmo nos limites de nosso Universo conhecido, e ilustra este princípio para o nosso Sistema Solar sob o olhar deste observador.
*O autor dedica este trabalho às Escolas Públicas municipais e estaduais, à Universidade de Brasília, à CAPES e ao CNPq, que permitiram seus estudos.
Resumo
0 nosso Sistema Solar quando visto por um observador nos limites de nosso Universo adquire dimensões que são tratadas pelos princípios da Física que regem o “Infinitamente Pequeno”. Quando esses princípios são aplicados, no quadro de um modelo, para o caso das órbitas planetárias são verificadas nas Leis de Kepler para o movimento dos planetas e suas respectivas distâncias médias ao Sol, bem como seus períodos de revolução. A maioria das órbitas dos satélites e anéis de saturno também são tratadas mostrando boa correlação com os resultados observados.
As constantes que aparecem no modelo são discutidas, indicando que uma única Constante e um conjunto de pequenos números inteiros, são suficientes para estabelecer as órbitas planetárias e respectivos períodos de revolução.
Uma constante adimensional de grandeza 10^{-40} aparece quando o cálculo realizado para determinar o raio da primeira órbita do átomo de Bohr e o autor indaga se um outro jogo de forças, além das forças gravitacionais, não regem também o nosso Universo, visto que esta mesma constante aparece em situações correlatas observadas pela Física.
Introdução
O emprego da numerologia sempre exerceu fascínio e despertou grande curiosidade entre os astrônomos na tentativa de estimar as distâncias dos planetas ao Sol. Na realidade desempenhou importante papel na descoberta dos planetas Urano (1781), Netuno (1846), do cinturão de asteroides (1801) entre os planetas Marte e Júpiter e do asteroide Quiron (1978) entre os planetas Saturno e Urano.
Consideremos inicialmente a Lei de Titius―Bode estabelecida em 1778 para estimar as distâncias planetárias:
D=0,4 +(0,3) \times 2^{n} U.A.
onde D é a distância para o n-ésimo planeta, e, uma Unidade Astronômica (U.A.) sendo igual à distância do planeta Terra ao Sol. Para Mercúrio devemos tomar D = 0,4 resultando assim para Vênus (n = 0),D = 0,7; para a Terra (n = 1), D = 1,0; para Marte (n = 2), D = 1,6 e assim por diante como mostrado na Tabela I:
TABELA I
| PLANETAS | LEI DE TITIUS-BODES | DISTÂNCIA REAL |
|---|---|---|
| Mercúrio | 0,4 | 0,3 |
| Vênus | 0,4 + 1 x 0,3 = 0,7 | 0,7 |
| Terra | 0,4 + 2 x 0,3 = 1,0 | 1,0 |
| Marte | 0,4 + 4 x 0,3 = 1,6 | 1,5 |
| – | 0,4 + 8 x 0,3 = 2,8 | – |
| Júpiter | 0,4 + 16 x 0,3 = 5,2 | 5,2 |
| Saturno | 0,4 + 32 x 0,3 = 10,0 | 9,6 |
| Urano | 0,4 + 64 x 0,3 = 19,6 | 19,2 |
| Netuno | 0,4 + 128 x 0,3 = 38,8 | 30,1 |
| Plutão | 0,4 + 256 x 0,3 = 77,2 | 39,5 |
Pela Tabela I podemos observar que a relação empírica dada pela Lei de Titius―Bode fornece distâncias precisas para os planetas interiores, mas começa a se mostrar imprecisa para Saturno, Urano e Netuno, não conseguindo prever a órbita de Plutão.
Vale a pena ressaltar que quando tal lei foi enunciada em 1778, não se conhecia nenhum planeta além de Saturno. A descoberta de Urano em 1781 cuja distância ao Sol, prevista empiricamente, estava de razoável acordo com sua distância real, suscitou entre os astrônomos indagações com respeito à lacuna correspondente ao algarismo 2,8 como apresentado na Tabela I. Talvez assim, poderia existir um novo planeta de pequeno tamanho e por esta razão não ainda, na época, descoberto. No período de 1801 a 1807, as pesquisas mostraram a existência destes pequenos ”planetas” que foram posteriormente chamados de asteroides, à distâncias médias de 2,8 Unidades Astronômicas como fornecidas pela Lei de Titius-Bode.
O asteroide Quiron foi previsto pelo astrônomo italiano Giuseppe Armellini que ao formular uma nova lei empírica em 1922 indicava a existência de um planeta justamente entre Saturno e Urano. Em 1978 o astrônomo norte-americano Charles T. Kowal descobriu o asteroide Quíron a uma distância ao Sol como aquela prevista a partir da lei empírica:
D=1,53^{n}
onde D (em U.A.), a distância média dos planetas ao Sol é dada em função dos valores de n que variam de n = -2 par Mercúrio; n E -1 para Vênus; n = 0 para a Terra; n = 1 para Marte e assim por diante como mostrado na Tabela II:
TABELA II
| PLANETAS | DISTÂNCIAS CALCULADAS | OBSERVADAS |
|---|---|---|
| Mercúrio | 1,53^{-2} = 0,43 | 0,39 |
| Vênus | 1,53^{-1} = 0,65 | 0,72 |
| Terra | 1,53^{-2} = 1,00 | 1,00 |
| Marte | 1,53^{0} = 1,53 | 1,52 |
| Vesta | 1,53^{1} = 2,34 | 2,36 |
| Camilla | 1,53^{2} = 3,58 | 3,48 |
| Júpiter | 1,53^{3} = 5,48 | 5,20 |
| Saturno | 1,53^{4} = 8,38 | 9,55 |
| Quiron | 1,53^{5} = 12,83 | 13,87 |
| Urano | 1,53^{6} = 19,63 | 19,20 |
| Netuno | 1,53^{7} = 30,03 | 30,11 |
| Plutão | 1,53^{8} = 45,94 | 39,52 |
Os asteroides Vesta e Camilla são representados na Tabela II como os limites do anel de cerca de dois mil asteroides cuja existência entre Marte e Júpiter foi prevista em 1766 pela Lei de Titius-Bode. De maneira análoga, Armellini, além de satisfazer as distâncias dos planetas e asteroides conhecidos, previu a existência de um outro asteroide que poderia estar situado entre Saturno e Urano.
O autor, no presente trabalho, objetiva apresentar um modelo para estabelecer as órbitas planetárias a partir de idéias e princípios que regem a Física Moderna, os quais certamente merecem algumas considerações sobre as grandezas observadas na natureza, suas respectivas unidades de medida e correlações no que diz respeito a aspectos de nossos Universos descritos como ‘Infinitamente Grandes” ou “Infinitamente Pequenos’. Para tal visualizamos no quadro abaixo algumas das grandezas pertinentes à ideia que será apresentada e em seguida propõe-se discutir sobre o que poderá ser inferido a partir de um determinado conjunto de observações e reflexões.
SOBRE O INFINITAMENTE GRANDE
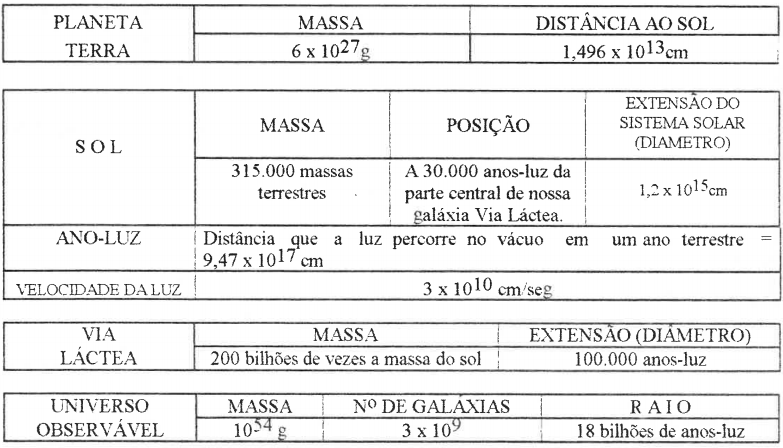
SOBRE O INFINITAMENTE PEQUENO
| MASSA DO ELÉTRON | 9,109 \times 10^{-28}g |
| CARGA DO ELÉTRON | 1,602 \times 10^{-19}C |
| MASSA DO PRÓTON | 1,672 \times 10^{-24}g |
| RAIO DE BOHR | 0,529 \times 10^{-8}cm |
| CONSTANTE DE PLANK | 6,625 \times 10^{-27}erg-seg |
| CONSTANTE DE BOLTZMAN | 1,38 \times 10^{-16}erg-k^{-1} |
Imaginemos então um observador que esteja localizado nos limites de nosso Universo Observável e que queira avaliar a massa de nosso planeta, tomando como referência para esta medida, a massa da Via Láctea como se esta fosse o nosso conhecido 1 Quilograma. Como resultado a massa solar seria avaliada em 5,0 \times 10^{ -12} Kg e a massa terrestre em aproximadamente 10^{ -17} Kg! E se tomarmos por sua vez pelo menos um dos conhecidos aglomerados de galáxias como referência, estes números seriam ainda menores! Este mesmo observador pode também estimar a extensão de nosso Sistema Solar, tendo como referência para esta estimativa, a extensão da Via Láctea tomando-a como se fosse, por exemplo, 1 metro.
Ele teria, como resultado, um número da ordem de 10^{-9} ml Então valeria a pena indagar se para este observador, caso ele estivesse interessado na maioria dos aspectos que regem os movimentos planetários em torno do Sol, se seriam exatamente aqueles mesmos fornecidos pelas leis que estamos habituados a empregar, ou seja, as Leis de Newton para os movimentos assim como a da Teoria Geral da Gravitação. E neste sentido o autor perguntaria, se para este universo infinitamente pequeno e então para aquele observador, se ele não tentaria estabelecer para o estudo em questão, alguns dos princípios que foram utilizados quando das descobertas dos mundos atômicos e sub-atômicos. Ou seja, em um primeiro passo, o observador poderia adotar um modelo similar aquele proposto por Bohr para a descrição das órbitas eletrônicas em sistemas atômicos e porque não, visto as dificuldades encontradas quando da utilização das leis que regem a Mecânica Clássica para O estudo proposto, atribuir mesmo, ondas de De Broglie a tão minúsculas massas observadas em tão minúsculas distâncias do Universo!
Como o referido observador não possui informações sobre o efeito da temperatura solar na formação das massas planetárias, ele poderia inferir que a todos os planetas fossem a eles atribuídas massas de mesmos valores, como também verificar a importância ou não desta aproximação com os resultados fornecidos pelo seu modelo exposto a seguir.
O MODELO
Como já conhecido, um dado planeta de massa m_{p} é mantido em sua órbita pela força gravitacional que o atrai em direção ao Sol. Tendo O Sol uma massa M_{s} essa força e (GM_{s}m_{p})/r^{2}, onde G é a Constante de Gravitação Universal, de acordo com a lei de Newton. Para um estado estacionário, ela deve compensar exatamente a força centrífuga m_{p}v^{2}/r , onde v é a velocidade orbital do planeta e r sendo sua distância ao Sol.
Desta forma:
\frac{m_{p}v^{2}}{r} = \frac{GM_{S}m_{p}}{r^{2}} (1)
ou seja,
m_{p}v^{2} = \frac{GM_{S}m_{p}}{r} (2)
De acordo com o princípio de dualidade onda-partícula de Louis de Broglie à toda partícula de momento p está a ela associada uma onda cujo comprimento de onda possui valor \lambda = h/p onde h é a constante de Plank. Atribuindo, neste mesmo sentido, ondas de De Broglie às massas planetárias m_{p} teremos:
\lambda = \frac{g^{*}}{M_{p}v} (3)
onde \lambda é o comprimento de onda associado ao planeta de massa m_{p}, possuindo movimento linear p de valor m_{p}v e g^{*} uma constante equivalente à Constante de Planck, que será discutida no final do presente trabalho.
A condição necessária para obter—se as órbitas estáveis de raio r terá que ser dada por:
2\pi r = n\lambda (4)
Com valores de n inteiros 1, 2, 3,…, para garantir assim uma representação de ondas estacionárias para as massas planetárias gravitando em torno do Sol. Da equação (3) obteremos:
m_{p}v = \frac{g^{*}}{\lambda} (5)
E da equação (4):
\lambda = \frac{2\pi r}{n} (6)
Substituindo a equação (6) na equação (5):
m_{p}v = \frac{ng^{*}}{2\pi r} (7)
mostrando que a intensidade do movimento angular L, para cada órbita, será dada por:
L = mvr = \frac{ng^{*}}{2\pi} (8)
Das equações (2) e (7)
(m_{p}v) v = (\frac{ng^{*}}{2\pi r}) v = \frac{GM_{s}m_{p}}{r}
a velocidade v será escrita então como:
v = \frac{2\pi GM_{s}m_{p}}{ng^{*}} (9)
e assim sendo o valor da distância r será fornecido a partir das equações (7) e (9)
r = \frac{ng^{*}}{2\pi m_{p}v}
ou seja,
r = \frac{n^{2}g^{*2}}{4\pi^{2}GM_{s}m_{p}^{2}} (10)
Cálculo do Período Orbital T
0 período de revolução T de um dado planeta pode ser obtido a partir da razão entre o perímetro orbital 2\pi r e sua velocidade v.
T = \frac{2\pi r}{v}
onde v e dada pela equação (9). Neste sentido:
T = (2\pi r) (ng^{*}/2\pi GM_{s}m_{p})
ou então
T = \frac{ng^{*}r}{GM_{s}m_{p}} (11)
Verificação das Leis de Kepler
a) Segunda Lei ou Lei das Áreas – “O segmento que une um planeta ao Sol descreve áreas iguais em tempos iguais”.
Ou seja, se designarmos por A a área total compreendida pela órbita de um dado planeta no seu período T de revolução em torno do Sol, a razão Área/Período deverá ser um número constante para aquela órbita. Como no presente modelo as órbitas são consideradas circulares, O valor de A será \pi r^{2} deveremos então calcular o valor de K_{2} = (A/T) onde K_{2} indica a constante acima mencionada e T sendo dado pela equação (11).
Assim sendo,
K_{2} = (\pi r^{2})/(ng^{*}r/GM_{s}m_{p}) = (\pi r)(GM_{s}m_{p}/ng^{*})
Como
r = \frac{n^{2}g^{*2}} {4\pi^{2}GM_{s}m_{p}^{2}}
K_{2} = (\frac{n^{2}g^{*2}\pi} {4\pi^{2}GM_{s}m_{p}^{2}}) (\frac{GM_{s}m_{p}} {ng^{*}})
Ou seja:
K_{2} = (\frac{ng^{*}} {2\pi} )( \frac{1} {2m_{p}})
Como dado pela equação (8) o momento angular L=mvr , para cada órbita; possui o valor ng^{*}/2\pi e assim expressa-se a constante K_{2} para a Segunda Lei de Kepler por:
K_{2} = \frac{L} {2m_{p}}
ou então
A/T = \frac{L}{2m_{p}}
mostrando que
A = (\frac{L} {2m_{p}})( T)
que é justamente a expressão que ilustra a Segunda Lei de Kepler como já demonstrada a partir das Leis de Newton e de Sua Teoria Geral da Gravitação.
b) Terceira Lei ou Lei Harmônica -”Existe uma relação constante entre o cubo da distância média de um planeta ao Sol e o quadrado do seu período de translaçăo“.
Se designarmos por K_{3} o valor da constante dada pela Lei Harmônica deveremos então calculá-la a partir do modelo ora apresentado.
Então para cada órbita:
K_{3} = r^{3}/T^{2}
onde os valores de r e T são dados pelas equações (10) e (11) respectivamente.
Assim,
k_{3} = r^{3}/(ng^{*}r/GM_{s}m_{p})^{2}
ou então,
K_{3} = r^{3}(GM_{s}m_{p}/n^{2}g^{*2}r^{2}) = (GM_{s}m_{p}/ng^{*})^{2}r;
Como
r = \frac{n^{2}g^{*2}} {4\pi^{2}GM_{s}m_{p}^{2}}
Teremos
K_{3} = (GM_{s}m_{p}/ng^{*})^{2} (n^{2}g^{*2}/4\pi^{2}GM_{s}m_{p}^{2})
ou seja
k_{3} = \frac{GM_{s}} {4\pi^{2}}
Visto este resultado, deverá ser verificado para cada órbita, a relação
\frac{r^{3}} {T^{2}} = \frac{GM_{s}} {4\pi^{2}}
que é na realidade a expressão para a Terceira Lei de Kepler, onde o valor da constante pode ser obtido pela Mecânica Clássica através da Teoria Geral da Gravitação de Newton e do conhecimento da Primeira Lei de Kepler ou Lei das Órbitas (”Os planetas giram ao redor do Sol, em Órbitas elípticas, ocupando este um dos focos da mesma”) como também da Segunda Lei ou Lei das Áreas (”O segmento que une um planeta ao Sol descreve áreas iguais em tempos iguais já apresentada anteriormente no presente trabalho. Para uma cuidadosa demonstração das expressões para as constantes das Leis de Kepler pela Teoria Geral da Gravitação de Newton ver por exemplo ”Classical Mechanics” por Herbert Goldstein, 1972 e “ Theoretical Physics”, por F. Woodbridge Constant, 1954.
Obtenção das distâncias médias planetárias e períodos orbitais a partir do modelo
0 objetivo desta seção é apresentar um procedimento que fornece as sucessivas Órbitas planetárias e respectivos períodos a partir do conhecimento de uma dada órbita.
Sejam dados, assim, duas Órbitas quaisquer correspondendo aos números inteiros n_{i} e n_{j} :
Assim:
r_{i} = \frac{n_{i}^{2}g^{*2}} {4\pi^{2}GM_{s}m_{p}^{2}} e r_{j} = \frac{n_{j}^{2}g^{*2}} {4\pi^{2}GM_{s}m_{p}^{2}}
e a razão r_{i}/r_{j} será dada por:
\frac{r_{i}} {r_{j}} = \frac{n_{i}^{2}} {n_{j}^{2}}
Para os períodos
T_{i} = \frac{n_{i}g^{*}r_{i}} {GM_{s}m_{p}}
Ou seja
T_{i} = \frac{n_{i}g^{*}} {GM_{s}m_{p}} (\frac{n_{i}^{2}g^{*2}} {4\pi^{2}GM_{s}m_{p}^{2}}) = n_{i}^{3} (\frac{g^{*3}} {4\pi^{2}GM_{s}^{2}m_{p}^{3}})
Pode-se então concluir que a razão entre os períodos de duas órbitas quaisquer pode ser escrita como:
\frac{T_{i}} {T_{j}} = \frac{n_{i}^{3}} {n_{j}^{3}}
E estabelecer o seguinte princípio:
“De modo geral, a razão entre as distâncias médias planetárias deverá obedecer a razão do quadrado dos números inteiros a ela associados e para os períodos a razão entre os cubos destes mesmos números inteiros.”
Então para órbitas sucessivas:
r_{i+1} = r_{i}(\frac{n_{i+1}} {n_{i}})^{2} (12)
E
T_{i+1} = T_{i} (\frac{n_{i+1}} {n_{i}})^{3} (13)
Se considerarmos, por exemplo, o nosso Sistema Solar e expressarmos em Unidades Astronômicas (onde a distância média da Terra ao Sol e respectivo período de revolução valem uma unidade) estes dados para o planeta Mercúrio, o de órbita mais interna, será então:
r_{1} = 0,3871 e T_{1} = 0,24
e em consequência as outras órbitas planetárias poderão ser obtidas a partir das relações (12) e (13), tomando n = 1 para o planeta Mercúrio como mostrado na Tabela III, n percorrendo de 1 a 10:
TABELA III
| n | r_{i+1} = r_{i} (\frac{n_{i+1}} {n_{i}})^{2} | T_{i+1} = T_{i} (\frac{n_{i+1}} {n_{i}})^{3} |
| 1 | r_{1} = 0,3871 | T_{1} = 0,24 |
| 2 | r_{2} = r_{1}(\frac{2} {1})^{2} = 1,5484 | T_{2} = T_{1} (\frac{2} {1})^{3} = 1,92 |
| 3 | r_{3} = r_{2}(\frac{3} {2})^{2} = 3,4839 | T_{3} = T_{2} (\frac{3} {2})^{3} = 6,48 |
| 4 | r_{4} = r_{3}(\frac{4} {3})^{2} = 6,1936 | T_{4} = T_{3} (\frac{4} {3})^{3} = 15,36 |
| 5 | r_{5} = r_{3}(\frac{5} {4})^{2} = 9,6775 | T_{5} = T_{4} (\frac{5} {4})^{3} = 30,0 |
| 6 | r_{6} = r_{5}(\frac{6} {5})^{2} = 13,9356 | T_{6} = T_{5} (\frac{6} {5})^{3} = 51,84 |
| 7 | r_{7} = r_{6}(\frac{7} {6})^{2} = 18,9679 | T_{7} = T_{6} (\frac{7} {6})^{3} = 82,32 |
| 8 | r_{8} = r_{7}(\frac{8} {7})^{2} = 24,7744 | T_{8} = T_{7} (\frac{8} {7})^{3} = 122,88 |
| 9 | r_{9} = r_{8}(\frac{9} {8})^{2} = 31,3550 | T_{9} = T_{8} (\frac{9} {8})^{3} = 174,96 |
| 10 | r_{10} = r_{9}(\frac{10} {9})^{2} = 38,710 | T_{10} = T_{9} (\frac{10} {9})^{3} = 240,00 |
Os resultados apresentados na Tabela III indicam que para que haja uma boa correlação entre as órbitas calculadas e aquelas conhecidas em nosso Sistema Solar, para os planetas mais internos, ou seja, aqueles de menores valores de momento angular, suas respectivas órbitas deverão Ser obtidas a partir de um conjunto de números associados ao valor de n de uma dada órbita e percorrendo OS valores do número zero até n .
Tomemos, por exemplo, os resultados verificados para o número n = 2. Os valores de m deverão ser então m = 0 ou m = 1 ou m = 2. Ou Seja, para o valor n = 2 deverá . Ser igualmente associado O número m = 2 que por sua vez a partir do par (n=2; m=2) pode-se obter as órbitas (n=2, m=1) e (n=2;m=0) através das seguintes relações:
r_{2,1} = r_{2,2} (\frac{2^{2} + 1^{2}} {2^{2}+ 2^{2}}) = 0,9677
E
r_{2,0} = r_{2,2} (\frac{2^{2}+0^{2}} {2^{2}+2^{2}}) = 0,7742
onde
r_{2,2} = 1,5484
Para os períodos:
T_{2,1} = T_{2,2} (\sqrt{\frac{5} {8}})^{3} = 0,9487
E
T_{2,0} = T_{2,2} (\sqrt{\frac{4}{8}})^{3} = 0,6788
onde
T_{2,2} = 1,92
Então para estas órbitas, em vez de um só número ser considerado, deverá ser levado em conta a soma dos quadrados dos números n e m ou seja n^{2} + m^{2} .
Outras órbitas correspondendo às distâncias médias reais de nosso Sistema Solar, obtidas a partir do procedimento acima mencionado são:
r_{1,1} = r_{2,0} \times (\frac{1^{2} + 1^{2}} {2^{2}+0^{2}}) = 0,7742 \times (\frac{2} {4}) = 0,3871
E
r_{3,2} = r_{3,3} \times (\frac{3^{2}+2^{2}} {3^{2}+3^{2}}) = 3,4839 \times (\frac{13} {18}) = 2,5161
e períodos
T_{1,1} = T_{2,0} \times (\sqrt{\frac{2} {4}})^{3} = 0,24
onde
T_{2,0} = 0,6788
T_{3,2} = T_{3,3} \times (\sqrt{\frac{13} {18}})^{3} = 3,98
onde
T_{3,3} = 6,48
Na Tabela IV são apresentados os resultados calculados para o nosso Sistema Solar a partir do modelo e suas considerações para as distâncias médias planetárias e respectivos períodos de revolução. Os valores são comparados com aqueles observados, em Unidade Astronômica até suas segundas casas decimais. O valor de K_{3} na Tabela IV indica o resultado para a Constante da Terceira Lei de Kepler, calculado para cada órbita a partir do modelo, também em Unidades Astronômicas, onde K_{3} = GM_{s}/4\pi ^{2} deverá ser igual a (1 \; distância \; astronômica)^{3}/(1 \; ano \; terrestre)^{2} .
TABELA IV
| POSIÇÃO | PLANETA OU ASTERÓIDE | r CALCULADO | r OBSERVADO | T CALCULADO | T OBSERVADO | K_{3} R^{3}/T^{2} |
|---|---|---|---|---|---|---|
| n=1 m=1 | Mercúrio | 0,39 | 0,39 | 0,24 | 0,24 | 1,03 |
| n=2 m=0 | Vênus | 0,77 | 0,72 | 0,68 | 0,62 | 0,99 |
| n=2 m=1 | Terra | 0,97 | 1,00 | 0,95 | 1,00 | 1,01 |
| n=2 m=2 | Marte | 1,55 | 1,52 | 1,92 | 1,88 | 1,01 |
| n=3 m=2 | Vesta | 2,52 | 2,34 | 3,98 | – | 1,01 |
| n=3 m=3 | Camilla | 3,48 | 3,58 | 6,48 | – | 1,00 |
| n=4 | Júpiter | 6,19 | 5,20 | 15,36 | 11,90 | 1,00 |
| n=5 | Saturno | 9,68 | 9,54 | 30,00 | 29,46 | 1,00 |
| n=6 | Quiron | 13,93 | 13,87 | 51,84 | – | 1,00 |
| n=7 | Urano | 18,97 | 19,18 | 82,32 | 84,01 | 1,00 |
| n=8 | – | 24,77 | – | 122,88 | – | 1,00 |
| n=9 | Netuno | 31,35 | 30,06 | 174,96 | 164,80 | 1,00 |
| n=10 | Plutão | 38,71 | 39,44 | 240,00 | 248,40 | 1,00 |
De modo geral, pode-se constatar uma correlação satisfatória entre os resultados calculados e observados. Vale a pena enfatizar que os cálculos realizados para as distâncias médias planetárias e períodos, como mostrados na Tabela IV, não foram levados em conta valores ou estimativas de massas planetárias para suas obtenções, ignorando completamente, a existência de planetas em nosso sistema Solar possuindo massas muitas vezes maiores que a massa terrestre: Júpiter (318,0 vezes); Saturno (95,2); Urano (14,6) e Netuno (17,3) e que por sua vez podem resultar possíveis efeitos de perturbações orbitais devido a maiores atrações gravitacionais com o Sol ou mesmo atrações mútuas entre eles. Ressalte-se, por exemplo, o planeta Júpiter que, com sua massa 318,0 vezes maior que a massa terrestre e 16 satélites entre luas e anéis correspondendo a 72% da massa total planetária, leva o autor a concluir, visto os resultados obtidos, que devido a este fato, um maior efeito atrativo dada a força gravitacional entre o Sol e Júpiter leva a aproximar a órbita deste planeta (previsto pelo modelo em aproximadamente 6,2 UA) a uma distância de 5,2 UA, resultando também em um menor período de revolução comparado aquele previsto pelos cálculos.
O autor desconhece os períodos de revolução dos asteroides Vesta, Camilla e Quíron, mas supõe fortemente que estejam corretos visto a boa concordância entre as distâncias médias calculadas e àquelas observadas e verificação da Lei Harmônica de Kepler para estes astros.
Finalmente, o modelo prevê a existência de um pequeno planeta ou asteroide na décima primeira posição na Tabela IV, correspondendo ao número inteiro n = 8, entre as órbitas de Urano e Netuno, a uma distância média de aproximadamente 25 UA do Sol e período de revolução de 123 anos terrestres.
Aplicação do modelo aos Anéis, Divisões e Satélites de Saturno
Graças às missões das naves espaciais Pioneer 11, Voyager 1 e Voyager 2 foram descobertos recentemente novos Satélites de Saturno além daqueles já conhecidos. Os pesquisadores em astronomia e astrofísica preveem ainda que novos outros satélites e anéis possam ainda serem descobertos. Entretanto, o modelo apresentado neste trabalho mostrou indicar concordâncias satisfatórias entre as órbitas observadas para os satélites de Saturno (do Anel C até o satélite Reia) e aquelas calculadas pelo procedimento de obtenção de órbitas sucessivas como mostrada anteriormente e cujos resultados são visualizados na Tabela V.
TABELA V
| ANÉIS E SATÉLITES DE SATURNO | DISTÂNCIA DO CENTRO DO PLANETA EM RAIOS DE SATURNO (OBSERVADO) | DISTÂNCIA DO CENTRO DO PLANETA EM RAIOS DE SATURNO (CALCULADO) |
|---|---|---|
| ANEL D (Lado Interior) | – | – |
| ANEL D (Lado Exterior) | – | – |
| ANEL C (Lado Interior) | 1,21 | R_{1} = 1,21 |
| ANEL C (Lado Exterior) | 1,53 | R_{2} = R_{1}(\frac{9} {8})^{2} = 1,53 |
| ANEL C (Lado Interior) | 1,53 | R_{2} = R_{1}(\frac{9} {8})^{2} = 1,53 |
| ANEL B (Lado Exterior) | 1,97 | R_{3} = R_{2}(\frac{10} {9})^{2} = 1,89 |
| ANEL A (Lado Interior) | 1,97 | R_{3} = R_{2}(\frac{10} {9})^{2} = 1,89 |
| ANEL A (Lado Exterior) | 2,26 | R_{4} = R_{3}(\frac{11} {10})^{2} = 2,28 |
| SATÉLITE 17 | 2,28 | R_{4} = R_{3}(\frac{11} {10})^{2} = 2,28 |
| SATÉLITE 16 | 2,31 | R_{4} = R_{3}(\frac{11} {10})^{2} = 2,28 |
| ANEL F (MEIO) | 2,32 | R_{4} = R_{3}(\frac{11} {10})^{2} = 2,28 |
| SATÉLITE 15 | 2,35 | R_{4} = R_{3}(\frac{11} {10})^{2} = 2,28 |
| SATÉLITE 11 | 2,51 | R_{5} = R_{4}(\frac{12} {11})^{2} = 2,72 |
| SATÉLITE 10 | 2,51 | R_{5} = R_{4}(\frac{12} {11})^{2} = 2,72 |
| ANEL G (MEIO) | 2,80 | R_{5} = R_{4}(\frac{12} {11})^{2} = 2,72 |
| MIMAS | 3,09 | R_{6} = R_{6}(\frac{13} {12})^{2} = 3,19 |
| ANEL E (Lado Interior) | 3,50 ou 4,00 | R_{7} = R_{6}(\frac{14} {13})^{2} = 3,70 |
| ENCELADO | 3,97 | R_{8} = R_{7}(\frac{15} {14})^{2} = 4,25 |
| SATÉLITE 13 | 4,91 | R_{9} = R_{8}(\frac{16} {15})^{2} = 4,84 |
| TÉTIS | 4,91 | R_{9} = R_{8}(\frac{16} {15})^{2} = 4,84 |
| SATÉLITE 14 | 4,91 | R_{9} = R_{8}(\frac{16} {15})^{2} = 4,84 |
| ANEL E (Lado Exterior) | 5,00 ou 6,00 | R_{10} = R_{9}(\frac{17} {16})^{2} = 5,46 |
| DIONÉIA | 6,30 | R_{11} = R_{10}(\frac{18} {17})^{2} = 6,12 |
| DIONÉIA B | 6,30 | R_{11} = R_{10}(\frac{18} {17})^{2} = 6,12 |
| – | – | R_{12} = R_{11}(\frac{19} {19})^{2} = 6,82 |
| – | – | R_{13} = R_{12}(\frac{20} {19})^{2} = 7,56 |
| RÉIA | 8,78 | R_{14} = R_{13}(\frac{21} {20})^{2} = 8,34 |
Para o caso dos anéis e satélites de Saturno, os resultados indicam que o conjunto de posições associadas às frações que percorrem de 1/2 até 8/7 correspondem à orbita na região do Anel D. Se tomarmos como uma primeira posição o lado interior do Anel C (a 1,21 raios de Saturno) e fizermos as frações percorrerem de 9/8 até 21/20 os cálculos efetuados mostram posições que de modo geral refletem as posições observadas do Anel C (lado exterior) até 0 satélite Réia, prevendo que possa existir órbitas reais nas posições 12 e 13 da Tabela V. Pode-se observar também que quando têm-se um conjunto de satélites e anéis em órbitas muito próximas umas das outras, praticamente em uma mesma região do espaço, as posições encontradas pelo procedimento são as mesmas.
Sobre a constante g^{*}
Vimos que, no quadro do modelo apresentado, para obter-se as distâncias dos planetas ao Sol, a partir de um conjunto de números inteiros e de uma constante que foi designada por g^{*} encontrou-se que:
r = \frac{n^{2}g^{*2}} {4\pi^{2}GM_{s}m_{p}^{2}}
Para efeito de uma melhor visualização dimensional, no panorama dos sistemas que estão sendo tratados, o autor propôs-se a trabalhar em um sistema de unidades que designou de UAC (Unidades Astronômicas de Cálculo) onde:
1 UA = Distância média da Terra ao Sol = 1,49 \times 10^{13} cm
1 AT = Um ano terrestre: Período de Revolução Sideral da Terra em torno do Sol = 3,154 \times 10^{7} seg
1 \; m_{t} = Uma massa terrestre = 6,0 \times 10^{27} g,
e que permitem escrever a Constante da Lei de Gravitação de Newton como:
G = 6,67\times10^{-8}cm^{3}g^{-1}seg^{-2} = 1,191\times 10^{-4}(UA)^{3}(m_{t})^{-1}(AT)^{-2}
Como mostrado anteriormente para O nosso Sistema Solar, algumas órbitas mais internas foram determinadas via um conjunto de números inteiros m associado ao número n que descreve uma dada órbita.
Se escrevermos para todas as órbitas as distâncias médias dadas por:
r = (\frac{n^{2}+m^{2}}{2}) \frac{g^{*2}}{4\pi^{2}GM_{s}m_{p}^{2}} (14)
com exceção das órbitas dos planetas Vênus (n = 2; m = 0) e Terra (n = 2; m = l) que foram obtidas a partir da órbita de Marte e do asteroide Vesta (n = 3; m = 2), que foi obtida a partir da órbita do asteroide Camilla, ao tomarmos m = n para o restante das órbitas, a expressão originalmente determinada para o cálculo das distâncias permanece inalterada posto que:
r = (\frac{n^{2}+n^{2}}{2}) \frac{g^{*2}}{4\pi^{2}GM_{s}m_{p}^{2}} = \frac{n^{2}g^{*2}} {4\pi^{2}GM_{s}m_{p}^{2}}
Como foi proposto, o modelo não leva em conta o efeito da temperatura Solar sobre a formação das massas planetárias. Dado que a massa total planetária é de 447 massas terrestres podemos assumir assim uma massa planetária média para cada um dos planetas/asteroides apresentados na Tabela IV, de aproximadamente 35 massas terrestres.
Assim, os resultados para os cálculos das distâncias, até suas terceiras casas decimais, como dados pela equação (14) e respeitando o par de números n e m para cada órbita, mostram que um único e exclusivamente único valor de g^{*} igual a 8,60\times 10^{2}(UA)^{2}(m_{t})(AT)^{-1} , permite obter os valores para as distâncias médias planetárias ao Sol como já exposto na Tabela IV. A Tabela VI ilustra estes resultados cujos cálculos foram determinados levando em conta os seguintes valores em UAC.
M_{s} = 3,315 \times 10^{5}
M_{p} = 35
G = 1,191 \times 10^{-4} (UA)^{3}(m_{t})^{-1}(AT)^{-2}
e
4\pi^{2} = 39,4784
Para esta Tabela, a_{0} corresponde ao valor da distância da primeira órbita, a do planeta Mercúrio, obtida como a seguir:
a_{0} = (\frac{1^{2}+1^{2}} {2}) \frac{(8,60\times 10^{2})^{2}} {39,4784\times 1,191\times 10^{-4}\times 3,315\times 10^{5}\times (35)^{2}}
Ou seja,
a_{0} = 0,387
E assim:
r=(\frac{n^{2}+m^{2}} {2}) a_{0}
TABELA VI
| POSIÇÃO | r = (\frac{n^{2}+m^{2}} {2}) a_{0} | CALCULADO | PLANETA / ASTEROIDE |
|---|---|---|---|
| n = 1 m = 1 | r_{1} = a_{0} = 0,387 | 0,387 | Mercúrio |
| n = 2 m = 0 | r_{2} = (\frac{2^{2}+0^{2}} {2}) a_{0} | 0,774 | Vênus |
| n = 2 m = 1 | r_{3} = (\frac{2^{2}+1^{2}} {2}) a_{0} | 0,967 | Terra |
| n = 2 m = 2 | r_{4} = (\frac{2^{2}+2^{2}} {2}) a_{0} | 1,548 | Marte |
| n = 3 m = 2 | r_{5} = (\frac{3^{2}+2^{2}} {2}) a_{0} | 2,515 | Vesta |
| n = 3 m = 3 | r_{6} = (\frac{3^{2}+3^{2}} {2}) a_{0} | 3,483 | Camilla |
| n = 4 m = 4 | r_{7} = (\frac{4^{2}+4^{2}} {2}) a_{0} | 6,192 | Júpiter |
| n = 5 m = 5 | r_{8} = (\frac{5^{2}+5^{2}} {2}) a_{0} | 9,675 | Saturno |
| n = 6 m = 6 | r_{9} = (\frac{6^{2}+6^{2}} {2}) a_{0} | 13,932 | Quiron |
| n = 7 m = 7 | r_{10} = (\frac{7^{2}+7^{2}} {2}) a_{0} | 18,963 | Urano |
| n = 8 m = 8 | r_{11} = (\frac{8^{2}+8^{2}} {2}) a_{0} | 24,768 | – |
| n = 9 m = 9 | r_{12} = (\frac{9^{2}+9^{2}} {2}) a_{0} | 31,347 | Netuno |
| n = 10 m = 10 | r_{13} = (\frac{10^{2}+10^{2}} {2}) a_{0} | 38,700 | Plutão |
Os resultados como apresentados na Tabela VI sugerem àqueles de cálculos de valores esperados de distâncias eletrônicas ao núcleo associados à orbitais atômicos do tipo s , obtidos a partir das funções de onda soluções da equação de Schrödinger tridimensional aplicada a átomos hidrogenoides. Sugerem também que estas funções possam vir a ser a soluções de uma equação similar à equação de Schrödinger bidimensional nas variáveis de posição r e angular \phi que apresentam a forma:
\Psi (r,\phi) = R(r)\Phi (\phi)
onde as funções na parte angular serão expressas por:
\Phi (\phi) = exp (im\phi)
que por sua vez serão auto-funções de um operador momento angular com a seguinte expressão para a equação de auto-valor:
L\Phi = \frac{mg^{*}} {2\pi}
e a função R(r) sendo solução da equação:
{ \frac{d^{2}} {dr^{2}} + \frac{1} {r} \frac{d} {dr} - \frac{m^{2}} {r^{2}} + \frac{2m_{p}} {g^{*2}} [E-V(r)] } R(r) = 0
Para a descrição, em Mecânica Quântica, da equação de Schödinger bidimensional,e suas possíveis soluções ver, por exemplo, ”Quantum Mechanics”, Capítulo IX, por Albert Messiah, 1974.
Para o caso da equação na parte radial acima escrita, a expressão para a energia potencial gravitacional é dada por:
V(r) = - \frac{GM_{s}m_{p}} {r}
e os auto-valores E para as energias poderiam assumir a seguinte forma:
E = - \frac{4\pi^{2}G^{2}M_{s}^{2}m_{p}^{3}} {2n^{2}g^{*2}}
Para estimar a expressão acima que poderá ser encontrada para os valores de E consideremos a energia total de um dado planeta
E = Energia Cinética + Energia Potencial
Energia Cinética = \frac{1} {2} m_{p}v^{2}
Da equação (2)
m_{p}v^{2} = \frac{GM_{s}m_{p}} {r}
Ou seja
E = \frac{GM_{s}m_{p}} {2r} - \frac{GM_{s}m_{p}} {r} = - \frac{GM_{s}m_{p}} {2r} (15)
Como
r = \frac{n^{2}g^{*2}} {4\pi^{2}GM_{s}m_{p}^{2}}
E substituindo em (15)
E = - \frac{4\pi^{2}G^{2}M_{s}^{2}m_{p}^{3}} {2n^{2}g^{*2}} (16)
Tomemos, por exemplo, a energia total gravitacional do planeta correspondente ao planeta Saturno cuja órbita está associada ao número inteiro n = 5 como dada classicamente:
E = - \frac{GM_{s}m_{p}} {2r} = - \frac{(1,19\times 10^{-4})\times 3,315\times 10^{5}\times 35} {2\times 9,68} = -71,37 UAC de energia
Como dada pela expressão (16):
E = - \frac{4\pi^{2}G^{2}M_{s}^{2}m_{p}^{3}} {2n^{2}g^{*2}}
= \frac{39,4784\times (1,191\times 10^{-4})^{2}\times (3,315\times 10^{5})^{2}\times (35)^{3}} {2\times(5)^{2}\times (8,6\times 10^{2})^{2}}
= -71,35 UAC de energia
Poderia-se indagar se O modelo, também, não permitiria fornecer as órbitas de um elétron em torno do próton como previsto pelo modelo atômico de Bohr para O átomo de hidrogênio. Com um pouco de exercício de paciência pode-se mostrar que a primeira órbita pode ser determinada, ou seja, r_{Bohr} = 0,528\times 10^{-8}cm para uma constante g^{*} irrisoriamente pequena de valor 3,25\times 10^{-83} (UA)^{2}(m_{t})(A_{t})^{-1} .
Pelo modelo de Bohr, qualquer órbita para O elétron é determinada pela equação:
r = \frac{n^{2}h^{2}}{4\pi ^{2}m_{e}e^{2}}
donde h = Constante de Planck
m_{e} = massa do elétron
e = carga do elétron
n = um número inteiro 1,2,3…
e para o presente modelo
r_{Bohr} = \frac{n^{2}g^{*2}} {4\pi ^{2} m_{e}^{2}GM_{p}}
Onde m_{e} = massa do elétron = 9,109\times 10^{-28}g
m_{p} = massa do prótron = 1,673\times 10^{-24}g
Podemos assim comparar as duas expressões:
\frac{n^{2}h^{2}} {4\pi^{2}m_{e}e^{2}} = \frac{n^{2}g^{*2}} {4\pi^{2}m_{e}^{2}GM_{p}}
ou seja
\frac{g^{*2}}{h^{2}} = \frac{GM_{p}m_{e}} {e^{2}}
que pode se reescrita:
\frac{g^{*2}}{h^{2}} = \frac{GM_{p}m_{e}/r^{2}} {e^{2}/r^{2}} = \frac{\left | \vec{F}_{g} \right |} {\left | \vec{F}_{e} \right |}
Onde \left | \vec{F}_{g} \right | intensidade da força gravitacional entre o próton e o elétron e \left | \vec{F}_{e} \right | = intensidade da força eletrostática entre o próton e O elétron, mostrando que:
g^{*} = (\frac{\left | \vec{F}_{g} \right | } { \left | \vec{F}_{e} \right |})^{1/2} \times h
Este resultado indica que a Constante g^{*} para o átomo de hidrogênio pode ser determinada, a partir de qualquer órbita conhecendo a razão entre a força gravitacional e a força eletrostática as quais o elétron está submetido e pela Constante de Planck cujo valor é 6,63\times10^{-27}cm^{2}.g.s^{-1} .
Como mencionado por Joseph Silk em livro de sua autoria “O Big Bang, a Origem do Universo“; no capítulo, Alternativas para 0 Big Bang:
“A gravitação e a força mais fraca do Universo. A razão entre a força gravitacional e a força elétrica, entre um elétron e um próton, tem o valor infinitesimal de aproximadamente 10^{-40} . Por que apareceria um número tão pequeno nas leis da Física relacionando essas duas forças fundamentais? Por uma coincidência das mais intrigantes, podemos encontrar um número de magnitude semelhante, a partir da razão entre duas escalas de tempo. Um número e a unidade de tempo para a luz atravessar uma distância igual ao raio clássico do próton. 0 outro número e a escala de tempo de Hubble. Essa razão adimensional e também de aproximadamente 10^{-40} . Por conseguinte, a razão entre duas forças fundamentais e a razão entre as escalas de tempo cósmica e atômica são da mesma ordem infinitesimal de magnitude. Poderia ser isso uma simples coincidência?
0 físico Paul Dirac, um dos fundadores da teoria quântica moderna, levantou, em 1957, a hipótese de que tal coincidência é tão notável que deveria ser aceita como uma das leis da natureza.”
Coincidentemente, é curioso constatar que a razão adimensional 10^{-40} aparece também neste trabalho quando determina—se o valor do raio de Bohr para 0 átomo de Hidrogênio, aplicando o modelo que permitiu obter as órbitas planetárias de nosso Sistema Solar. E se caso levarmos em conta a hipótese de Paul Dirac de que todas estas coincidências poderiam ser consideradas Como leis da natureza, não vislumbramos portanto, a existência de uma outra constante h^{*} , correlata à Constante de Planck, que também regesse O novo Universo? Visto esses fatos, poderíamos inclusive tentar avaliar o seu valor a partir daquele que foi empregado para g* quando da obtenção das órbitas como dadas pela Tabela VI.
se
h^{*} = (\frac{\left | \vec{F}_{e} \right | } { \left | \vec{F}_{g} \right |})^{1/2} \times g^{*}
onde
\frac{\left | \vec{F}_{e} \right | } { \left | \vec{F}_{g} \right |} = 10^{+40}
e
g^{*} = 8,6\times 10^{2} (UA)^{2}(m_{t})(AT)^{-1}
Assim:
h^{*} = 8,6\times 10^{22}(UA)^{2}(m_{t})(AT)^{-1}
que para o nosso observador deverá corresponder a valores bastante pequenos. Podemos ilustrar, como valor, tomando por exemplo, um ano terrestre como sendo 1 segundo, a dimensão da Via Láctea como 1 metro e a massa 1 quilograma e encontrar-se-á como resultado
h^{*} = 1,0\times 10^{-2} erg.seg
Caso esta Constante realmente existir o que poderá indagar-se é se a tal Constante não seria associada uma outra propriedade física que não seja somente as massas que constituem a matéria cósmica e que poderia descrever um outro tipo de força além das forças gravitacionais! De toda maneira, seria alentador saber que uma outra força fundamental poderia reger o destino de nosso Universo juntamente com as forças gravitacionais. Citamos mais uma vez Joseph Silk, em seu livro ”O Big Bang, A Origem
do Universo”, capítulo ”Uma Visão do Futuro Infinito” quando são comparadas as teorias existentes para a descrição de nosso Universo, aberto ou fechado, e que levam em conta somente o jogo das forças gravitacionais:
“Embora um universo aberto pareça ser a alternativa mais plausível, um universo aberto tem um futuro especialmente desagradável. Num universo aberto, as galáxias estão destinadas a se exaurir, e as estrelas a se consumirem, para nunca mais renascerem. A gravidade não mais poderá conter a expansão, e as forças gravitacionais se tornarão insignificantes nas escalas mais amplas. 0 espaço se tornará cada vez mais negro. 0 vazio entre os aglomerados de galáxias aumentará incomensuravelmente. À medida que os suprimentos de energia nuclear se exaurir, a matéria não será mais capaz de se opor à gravidade, em sistemas gravitacionalmente coesos. As galáxias, e em última análise até mesmo os grandes aglomerados, entrarão em colapso, para formar gigantescos buracos negros. Finalmente, toda a matéria se tornará extremamente fria, atingindo a temperatura do zero absoluto. Todas as forças se enfraquecerão e desaparecerão, até atingir-se um estado em que nada nunca mais mudará de novo. 0 espaço será infinito, e um futuro frio, negro e imutável estará inevitavelmente destinado a atingir todo o espaço. Esse destino só ocorrerá após bilhões e bilhões de anos, mas ele e, não obstante, inevitável num ,universo eternamente em expansão.”
“Uma especulação atraente (embora não comprovada) e a de que um universo fechado dará um novo salto e se expandirá novamente. Se isso ocorrer, o futuro do Universo será repetir todo o ciclo do Big Bang e formar novamente galáxias e estrelas.”
Então, se um outro tipo de força fundamental reger juntamente com as forças gravitacionais o futuro do Universo, poderíamos descartar o ameaçador e dramático destino, como aquele previsto para um Universo aberto, e teríamos esperança na repetição de todo o ciclo do Big Bang, ou seja, novas galáxias e estrelas seriam formadas e mais sagrado ainda, garantia da existência eterna da vida.
Conclusão
O autor propôs-se discutir os conceitos que regem os nossos Universos ditos “Infinitamente Grande” e “Infinitamente Pequeno” e refletir sobre a questão da observação que envolve esses Universos. A ideia origina-se do fato de que, quando assume-se como referência a Via Láctea tendo como parâmetro de medida o metro e o quilograma para sua dimensão e massa, respectivamente, assim, para um observador nos limites de nosso Universo é naturalmente atribuído para a massa terrestre e extensão de nosso Sistema Solar, grandezas tão infinitamente pequenas que levou-se a questionar se para esse observador as leis clássicas da Física forneceriam o todo dos aspectos que descrevem os movimentos planetários. Neste sentido foi proposto realizar tal estudo fundamentando-se nos princípios da Física Moderna que governam o Universo do Infinitamente Pequeno, utilizando um modelo análogo àquele de Niels Bohr para o átomo de hidrogênio, na antiga Teoria Quântica, empregando em seguida o principio da dualidade onda-partícula de Louis De Broglie onde atribuiu-se o caráter ondulatório às massas planetárias. Para o modelo apresentado, onde foi assumido órbitas circulares, foram verificadas as Segunda e Terceira Leis de Kepler para o movimento dos planetas. Pode ser igualmente obtido uni princípio que rege a obtenção das distâncias médias planetárias e respectivos períodos de revolução: “De modo geral, a razão entre as distâncias médias planetárias deverá obedecer a razão do quadrado dos números inteiros a elas associados e para os períodos a razão entre os cubos destes mesmos números inteiros”.
Os resultados obtidos para o nosso Sistema Solar bem como para a maioria dos satélites e anéis de Saturno indicaram boa concordância com os resultados observados.
Em seguida mostrou-se que uma única constante e um conjunto de pequenos números inteiros são suficientes para estabelecer as órbitas planetárias onde aquelas de menor valor de movimento angular são obtidos a partir de um espectro de números associados ao valor do número inteiro que descreve uma dada órbita. Tais resultados foram determinados empiricamente e sendo assim é natural que se aprofunde os estudos na direção de elucidar estes fatos apresentados.
Em uma tentativa de obter a primeira órbita do elétron para o átomo de Bohr através do modelo apresentado e quando compara-se com aquela estabelecida pelo modelo original verifica-se que uma constante adimensional de grandeza 10^{-40} conecta a Constante de Planck com a Constante “gravitacional”. Dado que esta mesma constante 10^{-40} é observada coincidentemente pela Física em diversas situações que não foram ainda elucidadas e que a partir deste fato o físico Paul Dirac levantou a hipótese de que “tal coincidência é tão notável que deveria ser aceita como uma das leis da natureza” levou o autor a indagar se um outro tipo de forças além das forças gravitacionais não atuam também no Universo. Estas “forças” poderia ser correlatas às nossas conhecidas forças eletrostáticas que variam com o inverso do quadrado das distâncias e que poderiam juntamente com as forças gravitacionais indicar os princípios que regem a trajetória de nosso Universo.
Finalmente, a partir das reflexões apresentadas e em consequência dos resultados obtidos deste estudo, leva o autor a concluir que como não existindo um olhar absoluto sobre a Natureza. o que é chamado de “Infinitamente Grande” pode se transformar em “Infinitamente Pequeno” e os princípios já estabelecidos pela Teoria Quântica juntamente com aqueles da Teoria da Relatividade de Einstein poderão enriquecer nossos estudos sobre o Cosmo e o destino de nosso Universo.
REFERÊNCIAS BIBLIOGRÁFICAS
1 N. Bohr, Phil. Mag. 26, l(l913).
2 ― L. De Broglie, Tese, Paris, 1924; Ann. de Phys. (10) 3, 22(1925).
3 ― E. Schrõdinger, Ann. d. Phys. 79, 734(1926).
4 — Pauling & Wilson, Introduction to Quantum Mechanics, MCGraw-Hill―KOgakuSha.
5 ― Albert Messiah, Quantum Mechanics, North-Holland Publishing Company.
6 — Herbert Goldstein, Classical Mechanics, Addison—Wes1ey Publishing Company, Inc.
7 — Ronaldo Rogério de Freitas Mourão, Da Terra às Galáxias, Uma Introdução à Astrofísica, Editora Vozes, Petrópolis.
8 — Romildo P. Faria, Flávio Alarsa, Aulos Platins Pimenta, Luis Antônio Alves Meira, Renato da Silva Oliveira e Walmir Thomazi Cardoso; Fundamentos de Astronomia, Editora Papirus, Campinas.
9 — Joseph Silk, O Big Banq, A Origem do Universo, Editora Universidade de Brasília.